在现代物理学的众多分支中,量子力学无疑是最为神秘和引人入胜的领域之一。它不仅改变了我们对物质本质的理解,还为我们提供了一种全新的方式来描述自然界的运作。在《张朝阳的物理课》中,谐振子模型的量子化问题是一个重要的讨论点,它不仅揭示了量子力学的基本原理,还展示了如何将经典物理概念转化为量子语言。
谐振子模型:从经典到量子
在经典物理学中,谐振子模型描述了一个物体在平衡位置附近的简谐振动,其运动可以用正弦或余弦函数来精确描述。然而,当我们将这一模型应用于微观粒子时,经典描述就不再适用了。量子力学告诉我们,微观粒子的行为受到不确定性原理的限制,这意味着我们不能同时精确知道粒子的位置和动量。
量子谐振子的能级
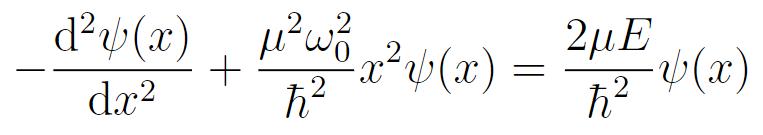
量子谐振子的能量不是连续的,而是以离散的能级形式存在。这些能级可以用量子数n来标记,n是一个非负整数。最低的能级(n=0)被称为基态,其能量不为零,这一现象被称为零点能。随着量子数n的增加,能量呈线性增加,这与经典谐振子的能量连续分布形成鲜明对比。
波函数与概率解释
在量子力学中,粒子的状态由波函数描述,波函数的平方模给出了粒子在某一位置出现的概率。对于量子谐振子,其波函数可以通过求解薛定谔方程得到。这些波函数是正交归一化的,意味着它们在数学上相互独立,且总概率为1。通过分析这些波函数,我们可以了解粒子在不同能级下的空间分布情况。
量子谐振子的应用
量子谐振子模型在物理学的多个领域都有广泛应用。例如,在固体物理学中,晶格振动可以用声子(即量子化的振动模式)来描述,这些声子就是量子谐振子的实例。在量子光学中,光场的量子化也涉及到谐振子模型,其中光子对应于谐振子的激发态。
张朝阳物理课的启示
通过《张朝阳的物理课》,我们不仅学习了量子谐振子的基本理论,还体会到了将抽象的量子概念与实际物理现象相结合的重要性。张朝阳通过生动的讲解和直观的示例,帮助我们理解了量子力学的深刻内涵,以及它在现代科技中的应用。
结论
量子谐振子模型是量子力学中的一个基础且核心的概念。它不仅展示了量子世界的奇异性,还为我们提供了一种理解微观粒子行为的有效工具。通过深入探究谐振子的量子化问题,我们能够更好地把握量子力学的精髓,并将其应用于解决实际的物理问题。《张朝阳的物理课》为我们提供了一个宝贵的学习平台,让我们能够更深入地探索这个充满奥秘的量子世界。











