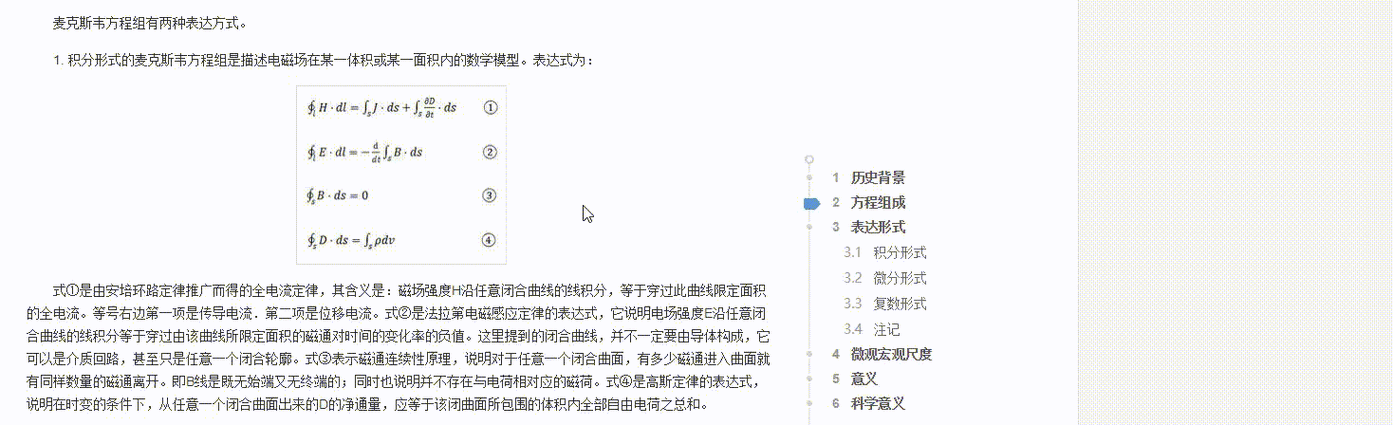
在现代物理学中,麦克斯韦方程组无疑是最为核心的理论框架之一,它不仅统一了电学和磁学,还预言了电磁波的存在。然而,当涉及到动态情况,即电场和磁场随时间变化,求解麦克斯韦方程组就变得尤为复杂。本文将跟随《张朝阳的物理课》的步伐,深入探讨如何求解一般情况下的麦克斯韦方程组,特别是在动态电磁势的背景下。
我们需要回顾麦克斯韦方程组的基本形式。在自由空间中,麦克斯韦方程组可以写作:
1. 高斯定律:∇·E = ρ/ε₀
2. 高斯磁定律:∇·B = 0
3. 法拉第电磁感应定律:∇×E = ∂B/∂t
4. 安培定律(含麦克斯韦修正项):∇×B = μ₀j μ₀ε₀∂E/∂t
其中,E是电场强度,B是磁感应强度,ρ是电荷密度,j是电流密度,ε₀是真空介电常数,μ₀是真空磁导率。
在动态情况下,电场和磁场不再是静态的,它们会随着时间变化,这就要求我们在求解方程组时必须考虑时间导数。为了简化问题,我们通常引入电磁势的概念。电磁势包括标量势φ和矢量势A,它们与电场和磁场的关系如下:
E = ∇φ ∂A/∂t
B = ∇×A
通过引入电磁势,我们可以将麦克斯韦方程组转化为关于电磁势的方程。例如,法拉第电磁感应定律可以转化为:
∇×(∇×A) = μ₀ε₀∂²A/∂t² ∇(∇·A μ₀ε₀∂φ/∂t)
这里,我们使用了矢量恒等式∇×(∇×A) = ∇(∇·A) ∇²A。为了进一步简化方程,我们可以利用洛伦兹规范条件:
∇·A μ₀ε₀∂φ/∂t = 0
这使得方程变为:
∇²A μ₀ε₀∂²A/∂t² = μ₀j
∇²φ μ₀ε₀∂²φ/∂t² = ρ/ε₀
这些方程被称为达朗贝尔方程,它们是波动方程的一种形式,描述了电磁势如何以波的形式传播。
我们将探讨如何求解这些方程。在实际应用中,我们通常会遇到边界条件和源分布的问题。为了求解达朗贝尔方程,我们可以采用分离变量法、格林函数法或者数值方法。例如,对于无界空间中的点源问题,我们可以使用格林函数来求解电磁势的解。对于有界空间,如在导电介质或边界附近,我们则需要考虑边界条件来确定解的唯一性。
在动态电磁势的背景下,我们还需要考虑电磁波的传播特性。根据麦克斯韦方程组,电磁波在真空中的传播速度为c = 1/√(μ₀ε₀),这是一个常数,与光速相同。这意味着,当我们求解动态电磁势时,我们实际上是在研究电磁波如何在空间中传播和相互作用。
我们将通过具体的例子来展示如何应用上述理论。例如,我们可以考虑一个点电荷在空间中运动的情况,通过求解达朗贝尔方程,我们可以得到电磁势的解,并进一步计算出电场和磁场。这个例子不仅展示了动态电磁势的求解过程,还揭示了电磁波与电荷运动之间的相互作用。
总结来说,《张朝阳的物理课》为我们提供了一个深入理解动态电磁势和麦克斯韦方程组的框架。通过引入电磁势和洛伦兹规范条件,我们将复杂的麦克斯韦方程组转化为波动方程,从而可以更好地理解和预测电磁现象。无论是在基础物理研究还是在工程应用中,这一理论都具有极其重要的意义。











